Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti:
TEMA I
Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti:
TEMA II
Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti
TEMA III
Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti
TEMA
“Il candidato discuta in modo chiaro e conciso uno dei seguenti argomenti:
TEMA
Il candidato sviluppi una delle seguenti tracce:
a) Interazione della radiazione con la materia (a scelta si descrivano gli aspetti fenomenologici oppure sperimentali oppure applicativi).
b) Il momento angolare in Meccanica Quantistica.
c) Vibrazioni reticolari nei solidi.
d) Illustrare un problema di modellistica fisica di propria conoscenza, evidenziandone in particolare gli aspetti computazionali.
TEMA
Il candidato tratti in modo chiaro e conciso uno dei seguenti punti:
1) I concetti di simmetria svolgono un ruolo fondamentale nella descrizione e nell'interpretazione di svariati fenomeni della fisica. Il candidato illustri in generale la potenzialità delle simmetrie e successivamente descriva uno o più fenomeni di particolare rilievo.
2) Lo "scattering" come mezzo di indagine della struttura dei sistemi fisici. Il candidato ne descriva le generalità e ne discuta un esempio.
3) Il candidato discuta uno o più fenomeni significativi riguardanti: interferenza o diffrazione o polarizzazione, nell'ambito della fisica classica o quantistica.
4) Il candidato discuta uno o più fenomeni riguardanti l'interazione radiazione-materia sia dal punto di vista teorico che sperimentale. Si scelga a piacere il tipo di sonda (fotone, elettrone ...) e campione.
5) Il candidato introduca il metodo variazionale in meccanica quantistica e ne discuta una o più applicazioni.
6) L'atomo di idrogeno. Il candidato discuta sinteticamente i risultati che si ottengono con l'equazione di Schrödinger. Introduca successivamente alcuni tipi di correzione a tale descrizione.
TEMA N. 1
Il candidato tratti in modo chiaro e conciso uno dei seguenti punti, facendo riferimento ad aspetti sperimentali e/o teorici:
a) Violazione della simmetria di parità P e della simmetria CP.
b) Il ruolo dei principi variazionali in Fisica Classica (ad es. in meccanica, in ottica, in elettromagnetismo o in relatività generale). Tempo permettendo, si discuta l'inquadramento del ''principio di minima azione'' in Fisica Quantistica.
c) Modelli a oscillatore in fisica.
d) Il gap di energia: origine, proprietà, metodi di indagine, conseguenze fisiche.
e) La costante dielettrica e/o la suscettività magnetica complessa e la loro dispersione in frequenza.
TEMA N. 2
Il candidato tratti in modo chiaro e conciso uno dei seguenti punti, facendo riferimento ad aspetti sperimentali e/o teorici:
a) La struttura a quark di mesoni e barioni
b) L'attuale descrizione delle interazioni fondamentali tra particelle elementari è basata sul principio di invarianza di gauge. Si discutano le differenze tra simmetrie "globali'' e simmetrie "locali'' con particolare riferimento ad almeno un modello fisico.
c) La diffrazione in fisica, con riferimento ad esempi significativi in ottica o in fisica quantistica.
d) La periodicità a livello microscopico è la proprietà fondamentale dei solidi cristallini: se ne discutano le principali caratteristiche e le conseguenze fisiche.
e) Le eccitazioni nella materia condensata (fononi, plasmoni, eccitoni, polaritoni, magnoni, ... ): il candidato discuta uno o più tipi di eccitazioni elementari, le relative proprietà e i metodi di indagine.
TEMA N. 3
Il candidato tratti in modo chiaro e conciso uno dei seguenti punti, facendo riferimento ad aspetti sperimentali e/o teorici:
a) L'esperimento di Rutherford è fondamentale per la nascita della fisica quantistica, tuttavia il calcolo della sezione d'urto per le particelle a su nuclei era basato sulla meccanica classica. Partendo da questo capitolo della storia della fisica, si discuta il passaggio dalla trattazione classica a quella quantistica dei processi d'urto.
b) L'analisi dimensionale costituisce uno strumento molto potente di indagine preliminare a disposizione del fisico. Si dia qualche esempio di applicazione tratto dalla fisica classica e dalla fisica quantistica.
c) Il ruolo della spettroscopia nella fisica del nucleo o delle particelle.
d) Le bande di energia: origine, proprietà, metodi di indagine, conseguenze fisiche.
e) Campi elettrici e magnetici nella materia: il candidato tratti uno o più casi di interesse fisico.
TEMA N. 1
Trattare in modo chiaro e conciso uno dei seguenti argomenti:
TEMA N. 2
Trattare in modo chiaro e conciso uno dei seguenti argomenti:
TEMA N. 3
Trattare in modo chiaro e conciso uno dei seguenti argomenti:
TEMA N. 1
Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti:
a) Principi di simmetria e leggi di conservazione giocano un ruolo guida nello sviluppo delle teorie fisiche. Il candidato discuta l'argomento, facendo riferimento ad uno o più casi specifici.
TEMA N. 2
Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti:
a) I processi di scattering come metodo d'indagine dei sistemi fisici.
TEMA N. 3
Il candidato tratti in modo chiaro e conciso uno dei seguenti argomenti:
a) Il progresso della fisica è stato spesso caratterizzato
dall'affermarsi di concetti di unificazione. Il candidato illustri l'argomento,
facendo riferimento ad uno o più esempi concreti.
b) La risposta dielettrica
dei solidi: modelli classici e quantistici e tecniche per la sua
deterrninazione, con riferimento ad un caso specifico.
c) Mostrare come un
modello teorico possa essere supportato o messo in crisi da un risultato di un
esperimento di fisica nucleare o subnucleare.
d) La teoria dei gruppi trova
applicazione nello studio di vari fenomeni fisici. Il candidato discuta
l'argomento, con riferimento ad uno o più esempi a lui più famliari.
TEMA N. 1
1) Il candidato svolga in modo chiaro e conciso
uno dei due argomenti seguenti:
- Si definisca e si discuta brevemente il
concetto di "Sezione d'urto". Si consideri la sezione d'urto per un processo
particolare, a scelta del candidato, e la si calcoli e/o si descriva l'apparato
sperimentale necessario per la sua misura. Si possono anche considerare sezioni
d'urto classiche come quelle per lo scattering Rutherford o lo scattering
Thomson.
- Si descriva un esperimento che consenta di determinare il momento
magnetico di una particella
TEMA N. 2
1) Il candidato svolga in modo chiaro e conciso
uno dei due argomenti seguenti:
- Il candidato descriva una tecnica
sperimentale o un formalismo matematico o un concetto teorico che abbia
contribuito allo sviluppo della fisica nella seconda metà del '900
- Si
descriva nel modo più preciso possibile un esperimento che consenta di
determinare il rapporto e/m fra la carica e la massa dell'elettrone.
2) Il candidato discuta concisamente (massimo una
pagina) due dei seguenti punti:
- Definizione di Lagrangiana ed Hamiltoniana
loro differenze
- Perdita di energia di particelle cariche pesanti (m >
me) nella materia
- Effetto Zeeman ed effetto Paschen-Bach
-
La radiazione di sincrotrone
TEMA N. 3
1) Il candidato svolga in modo chiaro e conciso uno dei due
argomenti seguenti:
- Il candidato discuta uno dei seguenti esperimenti:
- Esperimento di Michelson- Morley
- Esperimento di Rutherford
-
Esperimento di Stem e Gerlach
- Si descriva un esperimento che consenta di
misurare la suscettivita' magnetica di un materiale
2) Il candidato discuta concisamente (massimo una
pagina) due dei seguenti punti:
- Moto di una particella carica in presenza
di campi elettrici e magnetici
- Spettri rotazionali e vibrazionali di
molecole biatomiche
- Lo spin isotopico
- Diffrazione da una
fenditura
Temi d'esame A
M1A Calcolare la forza gravitazionale che agisce su una massa di prova m, collocata all'interno di una massa M distribuita uniformemente in una sfera di raggio R. Sia r<R la distanza della massa di prova dal centro della sfera.
M2A Note le densita' del ghiaccio rI = 0.917 gr / cm3, e la densita' dell' acqua marina rA =1.024 gr/cm3, determinare la frazione di volume visibile di un iceberg.
ElA Si calcoli il campo elettrico, in un punto qualsiasi dello spazio, dovuto a un filo rettilineo di sezione trascurabile e di lunghezza praticamente infinita, la cui densità di carica lineare è pari a l ues.
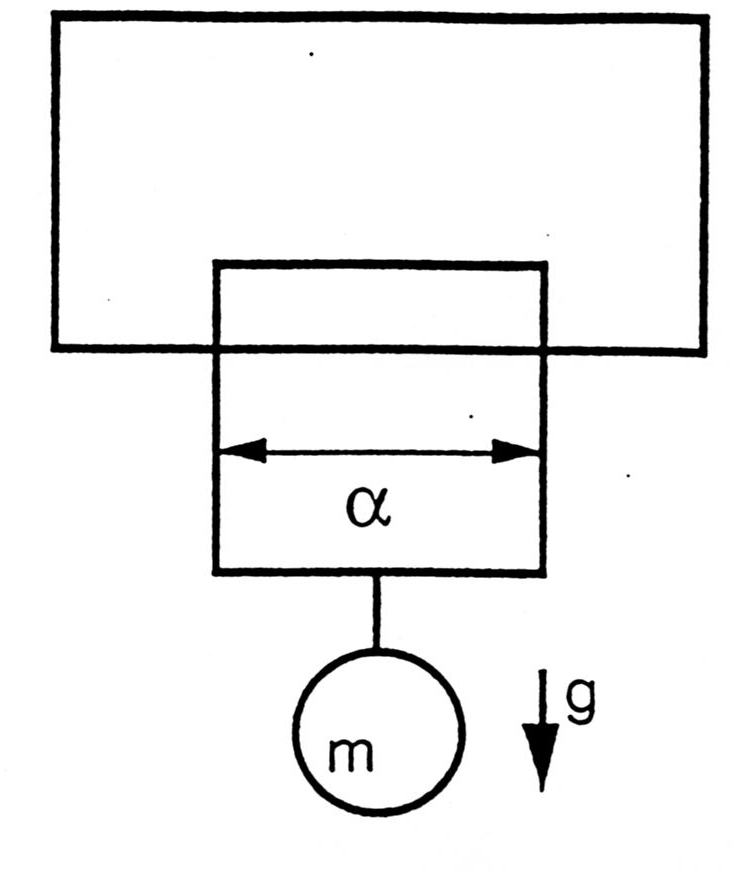
E2A A un circuito quadrato di lato a, costituito da un filo conduttore rigido e di massa trascurabile, è agganciato un corpo di massa m. Il circuto giace in un piano verticale rispetto al suolo e quindi sul corpo agisce il campo gravitazionale terrestre. Se un campo magnetico uniforme B attraversasse perpendicolarmente una porzione dell'area delimitata dal circuito, quale corrente dovrebbe percorrere il circuito affinchè risulti bilanciata la forza peso agente sul corpo?
| Il vettore B, entra perpendicolare nel piano del circuito. |
 |
R1A Si considerino due sistemi di riferimento inerziali, R e R' , in moto l'uno rispetto all'altro con velocita' relativa v. Da una rampa di lancio in R' parte un missile con inclinazione iniziale q' rispetto alla direzione (positiva) del moto dei due riferimenti. Si determini l'inclinazione iniziale di lancio q in R.
R2A Si consideri un'onda elettromagnetica piana. Si dimostri che la relazione che intercorre fra densita' di energia e densita' di quantita' di moto dell'onda e' la stessa che intercorre tra energia e quantita' di moto di una particella che si muova con la velocita' della luce.
N1A Consideriamo un fascio di
N=2·103 particelle che attraversa un contatore. Tenendo conto che la
probabilita' che una particella produca un conteggio sia
p=10-3,
determinare la probabilita' di avere tre conteggi.
N2A Si sono misurate due grandezze X ed Y con
errori s
a) Calcolare l'errore della grandezza somma S = X + Y
b) Calcolare l'errore della grandezza differenza D = X - Y
c) Calcolare l'errore della grandezza rapporto R = X / Y
N3A Dire cosa sono gli urti (scattering) Thompson e Rayleigh.
S1A Calcolare l'energia di un fotone della lunghezza d'onda di 5000 A.
S2A L'energia potenziale di due ioni in funzione della loro distanza può essere approssimata come:
U = (-ke2/r)+(b/r9). Si determini la forza in funzione di r e la distanza di equilibrio tra i due ioni.
S3A Calcolare la lunghezza d'onda di de Broglie di un neutrone avente un'energia cinetica di 0.05 eV.
T1A. Si consideri un sistema isolato descritto da una funzione d'onda y(r). Sia T(v) l'operatore di traslazione lungo il vettore v = (v1,v2,v3), definito da
T(v)y(r)=y(r+v). Si esprima T(v) in termini dell'operatore impulso.
T2A. Si consideri un sistema a tre livelli (E1=0; g1=2), (E2=2kT; g2=3), (E3=4kT; g3=1), dove con Ei, e con gi, i = 1,2,3, si sono rispettivamente indicate l'energia e la degenerazione dell'i-esimo livello. Se il numero totale di particelle nel sistema considerato e' N = 106 e le particelle sono distinguibili, si determini quale e' la distribuzione piu' probabile del numero delle particelle ni che occupano rispettivamente gli stati 1,2,3.
T3A. Si consideri il moto di una particella vincolata a muoversi lungo l'asse x in una buca di potenziale quadrata infinitamente profonda. All'istante t = 0 il sistema viene perturbato da un potenziale costante V0. Se la particella era inizialmente nel suo stato fondamentale, si determini la probabilita' di trovare la particella in uno stato eccitato n>1 all'istante t = t' > 0.
Temi d'esame B
M1B Calcolare il periodo di oscillazione che avrebbe una massa di prova m che attraversasse in caduta libera un pozzo ideale che connette due punti antipodali della Terra, sapendo che la costante universale di gravitazione e' G = 6.65·10-11 m3/(Kg s), che la massa della Terra e' M = 5.98·1024 Kg e che il raggio terrestre e' R = 6.4·106 m.
M2B Calcolare la velocita' quadratica media delle molecole di ossigeno allo stato gassoso alla temperatura di 300 K, sapendo che la massa molare dell'ossigeno e' M=0.032 Kg/mole, che la costante universale dei gas e' R = 8.31 J / mole . K , che la frazione delle molecole con velocita' compresa tra v e v+dv e'
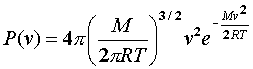
Si usi la formula di integrazione
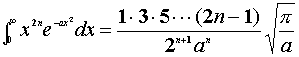
E1B Si calcoli la capacità di un condensatore costituito da 11 sottili fogli metallici ciascuno di area 500 cm2, separati l'uno dall'altro da carta paraffinata dello spessore di 5·10-4 m (eo = 8.85·10-l2 C2/m2N; er=2.6)
E2B Si ricavi il potenziale e il campo
elettrico in funzione di 
per un guscio sferico di raggio R la cui carica elettrica totale,
uniformemente distribuita, vale q.
R1B. Due astronavi A ed A' si muovono di moto rettilineo ed uniforme l'una rispetto all'altra con velocita' v. A' lancia verso A un razzo con velocita' u' e con inclinazione q' rispetto alla direzione (positiva) del suo moto rispetto ad A. Quale e' il valore di q misurato da A ?
R2B. Si consideri un' onda elettromagnetica piana. Si dimostri che il flusso di energia dell' onda e' diretto lungo la direzione di propagazione dell' onda, ed esprimere il vettore di Poynting in termini della densita' di energia del campo.
N1B Consideriamo un fascio di N = 2·103 particelle che attraversa un contatore. Tenendo conto che la probabilita' che una particella produca un conteggio sia p=10-3 , determinare la probabilita' di avere piu' di 2 conteggi.
N2B Si sono misurate due grandezze fisiche x ed y con errori sx e sy rispettivamente. Calcolare l'errore sulla grandezza U=x2- y2.
N3B Consideriamo un fascio di 6.25·1010 particelle a. per secondo. Calcolare l'intensita' di corrente del fascio. (e = 1.6·10-19 C )
S1B Calcolare la velocità di un elettrone la cui energia cinetica vale 2 Me V.
S2B Si stimi il modulo del momento di dipolo per una molecola di KCl sapendo che la distanza tra le cariche e r0= 2.79A, (Si asssuma il legame totalmente ionico)
S3B Su uno strato di materia spesso 5.0 mm incide normalmente un fascio di raggi X. Se il coefficiente di assorbimento lineare, per quella radiazione vale 0.07 mm, quale percentuale dell'intensità incidente attraversa lo strato?
T1B Si consideri in meccanica classica il moto di una particella in un campo Coulombiano. Si dimostri che il vettore px1-(l/r)r, e' un integrale primo del moto, ( r, p ed l indicano rispettivamente, il raggio vettore, la quantita' di moto, e il momento angolare della particella). Si discuta la possibilita' di misurare questo vettore quando si quantizza il moto della particella.
T2B Si consideri il moto di una particella di
massa m vincolata a muoversi lungo l'asse x sotto l'azione del potenziale U(x) =
+
per |x|> b,
U(x) = 0 per b/4 < |x|< b, U(x) = a per |x|< b/4 con b
ed a costanti assegnate. Applicando la teoria delle perturbazioni (primo
ordine) si determini il livello energetico piu' basso per questo sistema. Quale
ipotesi devo fare sulla costante a. per applicare la teoria delle perturbazioni
al primo ordine?
T3B Si consideri una collezione di particelle tutte caratterizzate dall' avere Lz=4(h/2p) e L2=18(h/2p)2. Si calcolino per questo sistema i valori di aspettazione <Lz> e <L2>.
Temi d'esame C
M1C Due particelle identiche realizzano un urto elastico nel sistema di riferimento in cui una di esse e' a riposo. Dire in quali condizioni le due particelle si muovono, dopo l'urto, lungo la stessa retta. Dire in quali condizioni si muovono, dopo l'urto, secondo direzioni ortogonali.
M2C Applicando il Teorema dell'Impulso di una forza, dimostrare che il principio dell'azione e reazione implica la conservazione della quantita' di moto totale.
E1C Una particella di carica + 10-10 C è posta all'origine di un sistema di riferimento cartesiano ortogonale, mentre una carica di -10-10 C viene posta nel punto di coordinate (6,0) m. Si calcoli il vettore E nel punto (3,4) m.
E2C Si calcoli l'energia di un guscio sferico di raggio R sul quale è uniformemente distribuita una carica elettrica totale q.
R1C In un grande laboratorio spaziale un osservatore sta esaminando una regione di spazio contenente soltanto un elettrone libero e isolato. Improvvisamente viene rilevata all'intemo di questa regione la presenza di un fotone g. Si dimostri che questo fotone necessariamente proviene dall' esterno della regione di osservazione.
R2C Si consideri una particella carica in moto sotto 1'azione di un campo elettromagnetico. Sotto quali trasformazioni dei campi elettrici e magnetici e' possibile far transitare la particella per gli stessi stati dinamici ma in ordine temporale inverso?
N1C Il risultato delle misure di due grandezze X ed Y si e' ottenuto con errori sx e sy rispettivamente.
a) Calcolare l'errore della grandezza somma S = X + Y
b) Calcolare l'errore della grandezza differenza D = X - Y
c) Calcolare l'errore della grandezza prodotto P = X Y
N2C Calcolo del tempo morto di un contatore di particelle. Siano R1, R2, R12 le frequenze di conteggi misurate da un contatore di particelle quando e' sottoposto rispettivamente ad una sola sorgente S1 alla sola sorgente S2 ed alle due sorgenti simultaneamente. Calcolare il tempo morto del contatore.
N3C Consideriamo un fascio di particelle a con intensita' di corrente 20 nA. Calcolare il numero di particelle a per secondo. (e = 1.6 . 1019 C )
S1C Si calcoli la funzione lavoro di un cristallo di K sapendo che la lugghezza d'onda massima per ottenere un'emissione di elettroni in un esperimento fotoelettrico è 5620 A.
S2C Un atomo viene eccitato rispetto al suo stato fondamentale mediante una transizione elettronica. Qual'è la minima indeterminazione dell'energia (DE) di questo stato se l' elettrone rimane in questo stato per 10-8 s ?
S3C Essendo S il momento angolare di spin e L il momento angolare orbitale dell'elettrone calcolare i possibili valori del momento angolare totale J per S = 1/2 e L = 3/2.
T1C. Si consideri un sistema di 4 particelle identiche i cui possibili livelli energetici siano Eo=0 eV, El=2eV , E2=4eV , E3=6eV , E4=8eV , E5=10eV, con rispettive degenerazioni g0=g1=g2=g3=2 , g4=g5=4. Se n 0=2, n1=n4=1, n2=n3=n5=0 , ( dove ni indica il numero di particelle nel livello i-esimo), si determini il numero delle possibili configurazioni del sistema nell' ipotesi che:
i) le particelle siano distinguibili,
ii) le particelle siano indistinguibili e obbediscano al principio di esclusione,
iii) le particelle siano indistinguibili e non obbediscano al principio di esclusione.
T2C Si consideri un sistema costituito da due elettroni con rispettive funzioni d'onda orbitali
Y1(r) e Y2(r). Si determini la funzione d'onda orbitale del sistema nell'ipotesi che:
(i) lo spin totale del sistema sia S = 0;
(ii) lo spin totale del sistema sia S = 1.
T3C Si consideri il moto di una particella di massa m
vincolata a muoversi lungo l'asse x sotto 1'azione del potenziale U(x) = + per
|x|> b, U(x) = 0 per b/4 < |x|< b, U(x) = a per |x|< b/4
con b ed a costanti assegnate. Applicando la teoria delle perturbazioni (primo
ordine) si determini il livello energetico piu' basso per questo sistema. Quale
ipotesi devo fare sulla costante a. per applicare la teoria delle perturbazioni
al primo ordine?
TEMA N.1
Il candidato tratti uno dei seguenti argomenti:TEMA N.2
Il candidato tratti uno dei seguenti argomenti:TEMA N.3
Il candidato tratti uno dei seguenti argomenti:
a)
Livelli elettronici nei solidi
b) Principi fondamentali e applicazioni dei
rivelatori a gas
c) Equazioni di Maxwell, potenziali elettromagnetici e
arbitrarieta' di gauge
d) La radiazione in una cavita' all'equilibrio
termico
e) I principi della quantizzazione dei campi.
TEMA N.1
Prima parteTEMA N.2
Prima parteTEMA N.3
Prima parte
a) Un protone e un antiprotone, a
distanza d, interagiscono attraverso l'interazione magnetica dipolo-dipolo. Si
ottengano gli autostati di spin totale in termini del momento magnetico del
protone. Si ricorda che il momento magnetico dell'antiprotone e' uguale a quello
del protone con segno negativo del rapporto giromagnetico.
b) Una pallina di
massa m, perfettamente elastica, rimbalza periodicamente su un piano muovendosi
lungo la verticale. Utilizzando le condizioni di quantizzazione alla
Bohr-Sommerfeld si ottengano gli autovalori.
c) Si consideri un circuito LC
in parallelo come possibile termometro attraverso la misura del valore
quadratico medio della tensione dovuta al rumore termico. Si stabilisca la
relazione di tale quantita' con la temperatura nei limiti di alte temperature e
di temperatura prossima allo zero assoluto.
d) Si ricavi,
nell'approssimazione classica, la potenza necessaria a mantenere la condizione
di stabilita' per una particella carica in moto su un'orbita circolare.
e)
Il candidato definisca la grandezza momento di quadrupolo nucleare.
Seconda parte
Lo sviluppo della Fisica e la costruzione del
complesso di conoscenze che ne e' alla base ha in larga misura avuto luogo in
maniera discontinua, a seguito di esperimenti o di analisi di gruppi di fenomeni
che hanno giocato un ruolo cruciale in tal senso. Il candidato descriva uno dei
seguenti esperimenti o effetti o fenomeni:
a) l'esperimento di Rutherford e
i modelli atomici;
b) l'esperimento di Rabi e il comportamento dei momenti
angolari;
c) l'effetto fotoelettrico e la quantizzazione del campo di
radiazione;
d) verifiche sperimentali dell'elettrodinamica quantistica;
e) lo stato di superconduzione;
f) principi di simmetria e leggi di
conservazione;
ne analizzi i risultati e ne descriva criticamente le
implicazioni concettuali.
TEMA N.1
Il candidato svolga uno o piu' dei seguenti temi:TEMA N.2
Il candidato svolga uno o piu' dei seguenti temi:TEMA N.3
Il candidato svolga uno o piu' dei seguenti temi:
1) Discutere approfonditamente le tecniche e i metodi di misura di
particelle neutre nell'ambito di un esperimento legato ai propri interessi di
ricerca.
2) Discutere l'importanza della rivelazione e della misura dei
leptoni in esperimenti di alte energie nello studio delle interazioni
fondamentali.
3) Illustrare il principio di invarianza di gauge e le sue
conseguenze.
4) La polarizzazione della luce. Applicazioni nel campo
della strumentazione fisica e nella diagnostica ottica di mezzi materiali.
5) Metodi spettroscopici per la caratterizzazione di strutture
cooperative (magnetiche o polari) e dei relativi processi di ordinamento in
solidi cristallini.
TEMA N.1
La risonanza in Fisica. Il candidato presenti il fenomeno prima nei suoi aspetti generali, sia classici che quantistici, e quindi in un campo di ricerca di suo interesse.TEMA N.2
Si illustri l'importanza che lo studio della interazione della radiazione (elettromagnetica e/o corpuscolare) con la materia ha avuto nella ricerca fondamentale e/o applicativa in Fisica.TEMA N.3
Stati legati della materia: il candidato esponga l'argomento trattandolo nel campo di ricerca di suo interesse.
TEMA N.1
1) Descrivete un esperimento in grado di misurare una o piu' caratteristiche del neutrino.TEMA N.2
1) Interazione del fotone con la materiaTEMA N.3
1) Descrivete un esperimento in grado di rivelare l'esistenza di struttura interna di uno stato osservato.